Complément 1.4
Page 46 - Établissement du diagramme d'espace-temps de la limousine et du garage.
1) D'abord un petit rappel en image pour se fixer les idées sur la contraction des longueurs.
Pour ce faire nous allons utiliser le personnage de Mr Tomkins inventé par le physicien Georges Gamow.
La vitesse de la lumière est ramenée à 30 km/h, ce qui permet à M. Tomkins sur son vélo d'appréhender
les différents phénomènes de contraction des longueurs et du temps.
(1) Le nouveau monde de Mr Tomkins
de Georges Gamow et Russel Stannard
Éditions Le Pommier - 2002
1-a) Lorsque Mr Tomkins (1) est dans son référentiel fixe il voit passer
un cycliste très aminci.

ce qui correspond au diagramme espace-temps ci-dessous pour le mètre-étalon dans la figure 1.5 avec ` OP = sqrt(1 - v^2) < OQ = 1 ` .
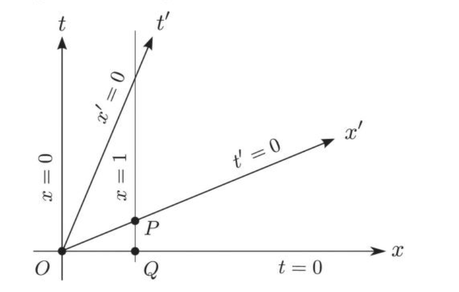
1-b) Lorsque Mr Tomkins est dans son référentiel mobile sur son vélo
il voit défiler les personnes et les batiments avec un aspect très aminci.
Dans les deux cas Mr Tomkins est immobile dans son référentiel (même
s'il pédale sur son vélo ! ).

ce qui correspond au diagramme espace-temps ci-dessous pour le mètre-étalon aussi avec ` OQ = sqrt(1 - v^2) < OP = 1 ` dans la figure 1.6 .

Pour revenir au problème de la grosse limousine de Lenny qui pourrait éventuellement tenir dans le petit garage de Art, il est clair maintenant que, comme le garage de Art est tout juste légèrement plus grand que 4,3 mètres et que la limousine de Lenny est deux fois plus grande, soit 8,6 mètres, c'est le cas 1-a) qui peut se présenter favorablement dans le référentiel fixe de Art. Par contre il est sûr que la limousine de 8 mètres ne tiendra pas dans un garage plus petit que 4 mètres dans le référentiel en mouvement de Lenny. Par le calcul du cas 1-a), et après être revenu en unités conventionnelles : ` x^' = x sqrt(1 - frac{v^2}{c^2}) ` avec : ` x = 8,6 ` m ` v = 276\ 800 ` km/s ( c'est plus compréhensible que les m/s ) ` c = 300\ 000 ` km/s soit : ` frac{v^2}{c^2} = frac{(276\ 800)^2}{(300\ 000)^2} = 0,85 ` ` x^' = 8,6 sqrt(1 - 0,85) = 8,6 sqrt(0,15) ` ` x^' = 3,33\ "m" ` et donc bien ` <\ 4 ` m Ensuite l'objectif est de savoir reconstruire la figure 1.9 page 46, car en regardant d'un peu plus près, les différentes étapes nécessaires ne m'ont pas sauté aux yeux. 2) Le commencement est une évidence mais il faut la nommer. Quel est mon diagramme espace-temps lorsque je suis immobile ?
Si je suis immobile par exemple à 2 mètres du début d'un trottoir,
pris comme référence, ma position dans le temps va être :
t = 0, x = 2 m point A
t = 1, x = 2 m point B
t = 2, x = 2 m point C
t = 3, x = 2 m point D
t = . . x = 2 m
ce qui donne le diagramme ci contre.
C'est donc une droite parallèle à l'axe Ot en x = 2.
Et la position de la porte d'entrée du garage de Art ainsi que le fond
de son garage profond de 4 m vont être représentés de cette manière.
Ce qui donnera donc deux droites espacées de 4 m.

3) Maintenant, comment représenter le mouvement de la voiture de Lenny
dans son diagramme espace-temps ?
Sa position varie dans le temps avec une vitesse ` v ` .
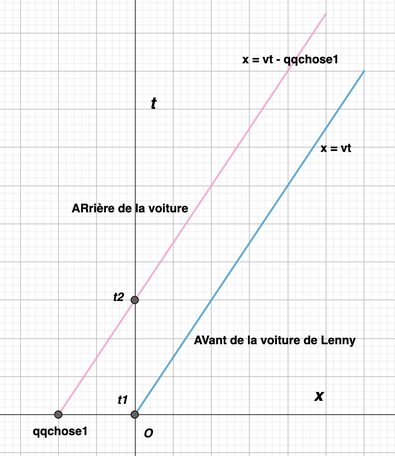
Et elle va donc se déplacer suivant la droite ` x = vt ` .
Plus exactement Art va d'abord voir passer l'AVant de la voiture de Lenny
au temps ` t_1 ` et ensuite l'ARrière de la voiture quelques instants
après au temps ` t_2 ` vu la longueur de la voiture et sa vitesse.
Ce qui va donner une autre droite ` x = vt - qqchose_1 `
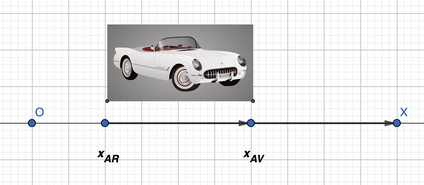
Dans le mouvement de la voiture de Lenny sur l'axe ` Ox `
l'arrière de la voiture est toujours derrière l'avant :
` x_(AR) = x_(AV) - qqchose_2 `
Si la voiture de Lenny est au repos dans le référentiel de Art, on a :
` qqchose_2 = 8,60 ` m .
Par contre, dans notre cas, Art immobile sur le trottoir voit passer la voiture de Lenny
à toute vitesse dans la rue jusqu'au garage.
Il va donc la voir amincie. C'est le cas 1-a) .
La longueur de la voiture perçue par Art est celle que nous avons calculée
au début, soit ` 3,33 ` m .
Ce qui nous donne notre ` qqchose_1 ` recherchée :
` qqchose_1 = 8,60 sqrt(1 - frac{v^2}{c^2} ) = 3,33 ` m
4) Nous pouvons maintenant construire les diagrammes espace-temps correspondant à notre problème. La voiture de Lenny va t'elle pouvoir tenir dans le garage de Art malgré sa longueur apparemment trop grande ? Nous voyons donc qu'au point " b ", l'arrière de la voiture de Lenny a franchi la porte d'entrée du garage de Art. Il nous faut maintenant considérer les différentes surfaces de simultanéités . Ce sont donc respectivement le segment bc pour Art parallèle à l'axe Ox, et la droite bx" pour Lenny. On se souvient que toutes les positions des points sur une surface de simultanéité correspondent à un même instant ` t ` pour le référentiel concerné. On voit alors que pour le référentiel de Art, l'avant de la voiture de Lenny est en " c1 ", donc à l'intérieur du garage, avec son arrière en " b " à l'entrée du garage et on peut dire qu'à cet instant la voiture de Lenny vue par Art est contenue entièrement dans le garage. Par contre, pour le référentiel de Lenny, l'avant de sa voiture est en " e ", donc à l'extérieur du garage, et on peut dire qu'à cet instant heureusement que la porte de derrière du garage est ouverte ! Dans un cas comme dans l'autre, la porte de derrière du garage doit rester ouverte, car même si Art voit la voiture de Lenny dans le garage, ce n'est que grace à son mouvement très rapide qui ne s'arrêtera pas. Et cette vision ne durera qu'un court instant.
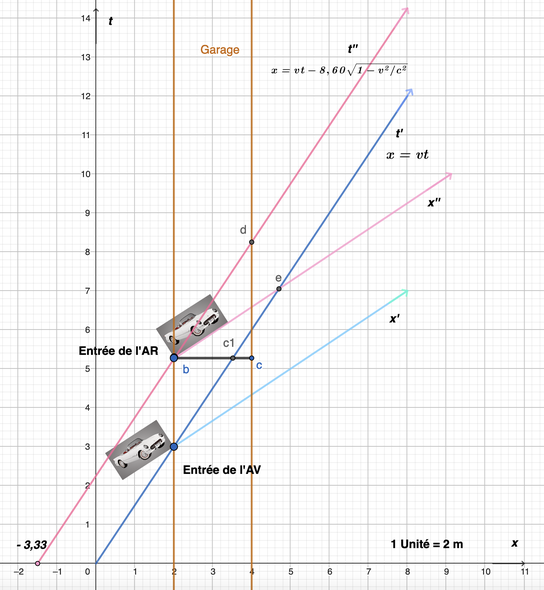
Comme pour Mr Tomkins qui ne voit pas son vélo changer de taille dans son référentiel, Lenny voit toujours sa voiture avec une longueur de ` 8,60 ` m .
